
To end it, we should return to your first position and then stop until the data gathering ends. After that, you should move quickly in front and then stop immediately at t=7 to t=9. This graph suggests no movement from t=0 to t=2, move away from t=2 to t=5, and then move to your previous position and stationary again at t=5 to t=7. 5m, the base line will always be at zero. It means that no matter where you are, whether 0. In addition to that, it moves smoothly to and fro thus making it look like a wave.Ĭomputing for the Average velocity: Motion 8 Graph Analysis: In this graph, the dependent is the velocity. Computing for the person’s velocity, at t=0 to t=2 = At t= 2 to t=4, For the acceleration Motion 7 Graph Analysis:The motion described in this graph is a motion that forms a sine or cosine curve meaning that it is periodic. Motion Graph 2 Analysis: The motion described in this graph is a motion at increasing velocity (constant acceleration). At t=2 to t=4, = At t=6 to t=8 (Note:The answer is negative because the person is moving towards the detector) Velocity at t= 0 to t=2, t=4 to t=6 and t=8 to t=10 is 0. Finally, at t=8, the person stayed at rest again for another 2 seconds. 3 meters backward at a constant velocity the person then stayed at rest again for another 2 seconds and then started moving 0. Use the Finding slopes accurately pages to help you do this.

Find the coordinates of the two points where your line intersects the graph’s edges. Extend the line you draw to the boundaries of the graph. Then at t=2, the person started moving about 1. t graph draw with a straight edge a straight line that best passes through the data. 7 meters away from the detector, and stay at rest for 2 seconds. Motion Graph 1Īnalysis: The motion described in this graph is a motion that starts about 0. The person being detected follows, as similarly as possible, the trend of motion in the default graph – hence graph matching. (If wealth were equally distributed, the Lorenz curve would be a. A Lorenz curve for wealth in a population tells, for example, that the least wealthy 50 of the population owns 10 of the wealth. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. Fractile graphical analysis is an important generalization of the method and use of concentration (or Lorenz) curves. We recommend using aĪuthors: Paul Peter Urone, Roger Hinrichs Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the

The velocity increases until 55 s and then becomes constant, since acceleration decreases to zero at 55 s and remains zero afterward. 0 m/s 2 to zero when the car hits 250 m/s. (This was the final velocity of the car in the motion graphed in Figure 2.48.) Acceleration gradually decreases from 5. Time again starts at zero, and the initial velocity is 165 m/s. Now consider the motion of the jet car as it goes from 165 m/s to its top velocity of 250 m/s, graphed in Figure 2.51. Graphs of Motion Where Acceleration is Not Constant Further experiments are then performed to determine the validity of the hypothesized relationships. From such graphs, mathematical relationships can sometimes be postulated.

Correlations imply physical relationships and might be shown by smooth graphs such as those above. are one of our most useful tools when describing motion they are often used to determine if relationships exist between quantities. In fact, an important way to discover physical relationships is to measure various physical quantities and then make graphs of one quantity against another to see if they are correlated in any way. It is not accidental that the same equations are obtained by graphical analysis as by algebraic techniques. Notice that this equation was also derived algebraically from other motion equations in Motion Equations for Constant Acceleration in One Dimension.
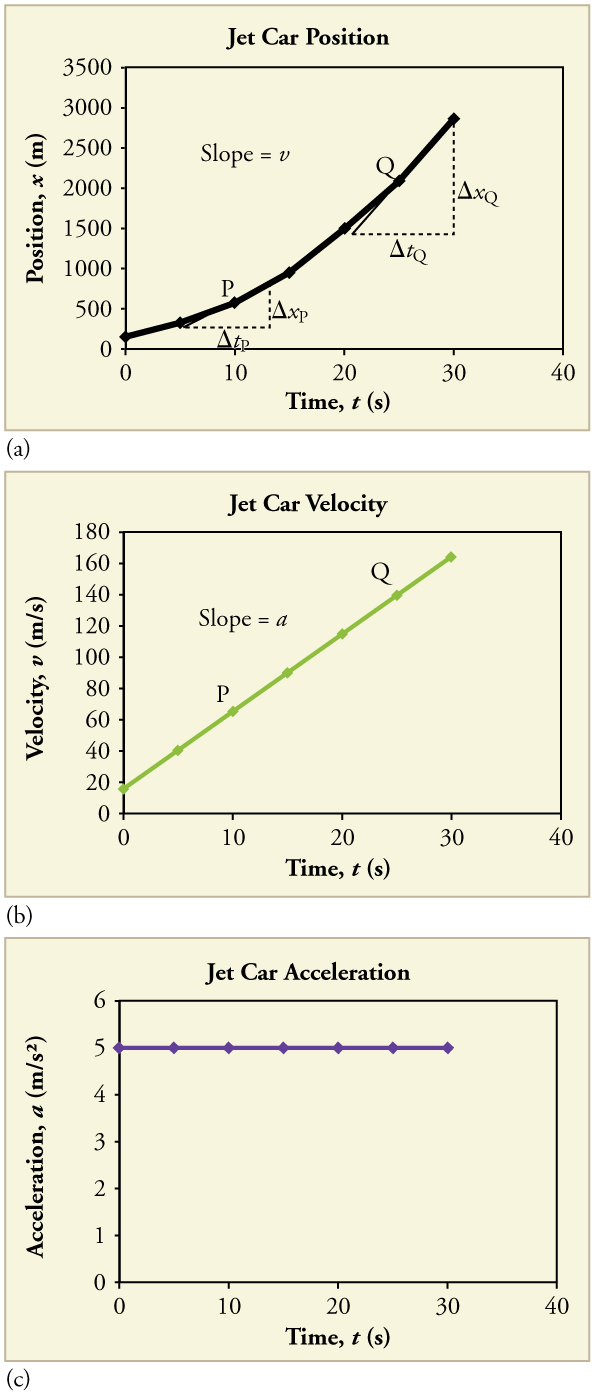
A general relationship for velocity, acceleration, and time has again been obtained from a graph.


 0 kommentar(er)
0 kommentar(er)
